Dynamics: Perspectives from Linear Algebra

Dynamical Systems

A dynamical system is any system that:

• has a state representing the relevant condition that the system is in
• an evolution rule that describes the future state as a deterministic function of the current state

The state could be any variable whose evolution we would like to keep track of (temperature of a city, economy-wide inflation rate, position of a vehicle). We usually represent the state as a vector. We will restrict the discussion to deterministic systems as the analysis is much simpler and the intuition mostly carries over to stochastic systems.

Consider a simple system governed by the equation: \(\dot{x_t}=Ax_t\)

The rate of change of the state is a linear function of the current state.

In general, any matrix $A$ can be written (uniquely) as the sum of a Hermitian (a matrix that is equal to its conjugate transpose) and Skew-Hermitian matrix (equal to the negative of its conjugate transpose):

\[A=S+K\]

\(S=\frac{A+A^*}{2}\) and \(K=\frac{A-A^*}{2}\)

Define \(\text{Energy}=x^*x=\mid\mid x_t\mid\mid^2\)

Now we’re done. Let’s break down a concrete example with a 2×2 matrix and see how the symmetric and skew-symmetric parts affect the dynamics.

---

Pick a dynamics matrix:

\[A=\begin{bmatrix}−2 & 3\\ −3 &−2\\ \end{bmatrix}\]

Step 1: Compute S

\[S=\frac{A+A^*}{2}=\begin{bmatrix}−2 & 0\\ 0 &−2\\ \end{bmatrix}\]

---

Step 2: Compute K

\[K=\frac{A-A^*}{2}=\begin{bmatrix}0 & 3\\ -3 &0\\ \end{bmatrix}\]

Interpretation:

So now we have:

• S: pulls the system radially inward (shrinks all directions equally)

• K: rotates vectors counterclockwise (since it looks like a 90° rotation matrix scaled by 3)

What happens to the dynamics?

The system:

\[\dot{x}=Ax=Sx+Kx\]

is a combination of:

• Exponential decay from S

• Rotation from K

This gives a spiraling trajectory into the origin — a stable focus.

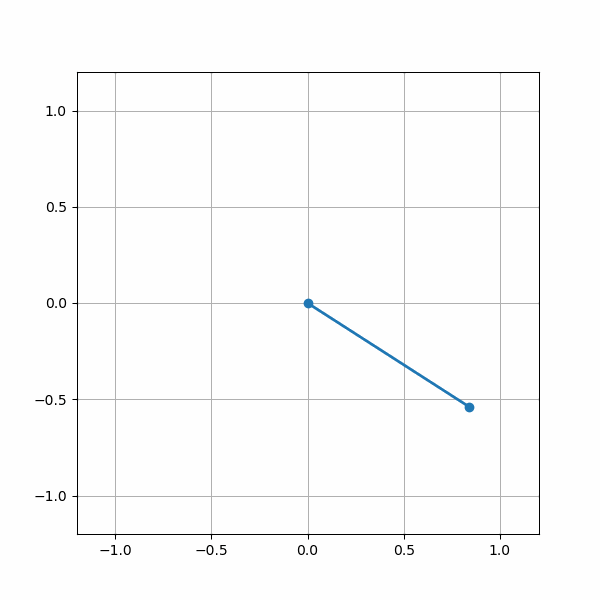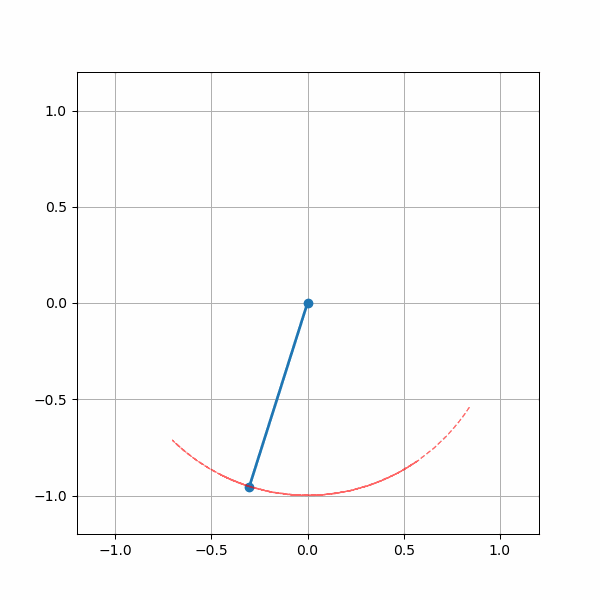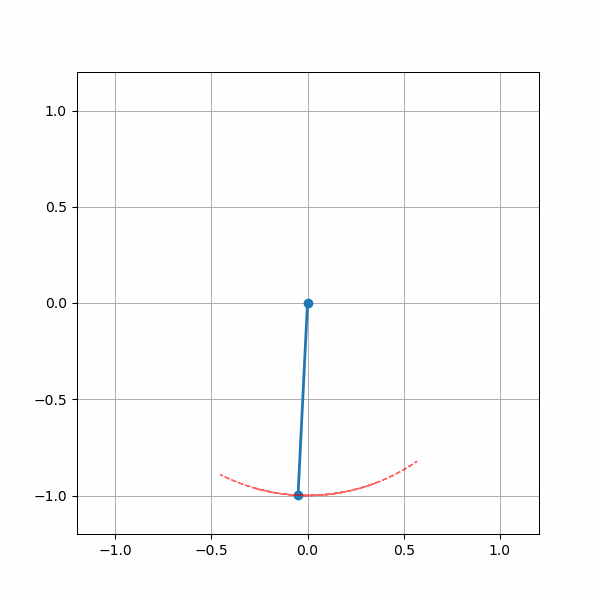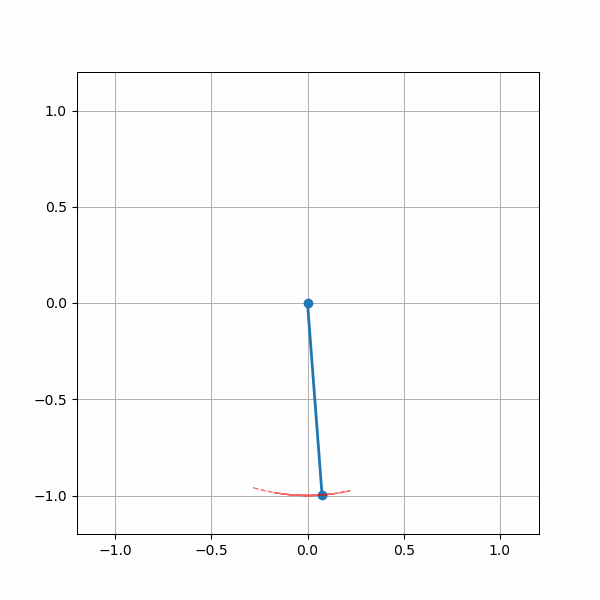
We can simulate this with initial condition \(x(0)=\begin{bmatrix} 1 \\ 0 \end{bmatrix}\), and the trajectory will look like a spiral winding into zero, rotating counterclockwise.

Energy decay

Let’s check the rate of change of \(\mid\mid x_t\mid\mid^2\):

\(\frac{d}{dt}\mid\mid x(t)\mid\mid^2=2x^TAx=2x^TSx=2(−2x^Tx)=−4\mid\mid x_t\mid\mid^2\)⇒Exponential decay!

A state-space model of a damped pendulum

If we denote the state of the system by the angle that the pendulum makes with the vertical axis, we can easily write the differential equation governing its change:

Equation of Motion (Nonlinear)

The equation for a pendulum of mass m, length $\ell$, under gravity $g$, with damping coefficient $b$ is:

\[m \ell^2 \ddot{\theta} + b \dot{\theta} + mg\ell \sin(\theta) = 0\]

Divide through by $m \ell^2$:

\[\ddot{\theta} + \frac{b}{m \ell^2} \dot{\theta} + \frac{g}{\ell} \sin(\theta) = 0\]

Define:

• $\omega=\dot{\theta}$ (angular velocity)
• $\theta$: angular position

Then we write the nonlinear state-space form:

\[\begin{bmatrix} \dot{\theta} \\ \dot{\omega} \end{bmatrix}= \begin{bmatrix} \omega \\ \frac{b}{m \ell^2} \omega - \frac{g}{\ell} \sin(\theta) \end{bmatrix}\]

Linearize Around the Equilibrium (θ=0)

When θ≈0, we use sin⁡(θ)≈θ. Then the system becomes linear:

\[\begin{bmatrix} \dot{\theta} \\ \dot{\omega} \end{bmatrix}=\begin{bmatrix} \omega \\ -\frac{b}{m \ell^2} \omega - \frac{g}{\ell} \theta \end{bmatrix}\]

Define state vector:

\(x=\begin{bmatrix} \theta \\ \omega \end{bmatrix}\) \(\dot{x}=Ax\)

With:

\[A = \begin{bmatrix} 0 & 1 \\ -\frac{g}{\ell} & -\frac{b}{m\ell^2} \end{bmatrix}\]

Decompose Matrix $A$

Let’s identify the rotational vs. dissipative components.

Let:

• $\alpha=\frac{g}{\ell}$

• $\beta=\frac{b}{m\ell^2}$

Then:

\[A = \begin{bmatrix} 0 & 1 \\ -\alpha & -\beta \end{bmatrix}\]

Now split into symmetric + skew-symmetric parts:

\[S = \frac{1}{2} \begin{bmatrix} 0 & 1 - \alpha \\ 1 - \alpha & -2\beta \end{bmatrix}\\ K = \frac{1}{2} \begin{bmatrix} 0 & 1 + \alpha \\ -(1 + \alpha) & 0 \end{bmatrix}\]

Key Points

• The skew-Hermitian part K captures the rotational part of the dynamics. This just rotates the state-space. The distance of the phase-point (captured by $x$) from the origin remains fixed. This is called the conservative part of the dynamics.

• The Hermitian part S has negative diagonal entries (if $\beta >0$), introducing damping — i.e., energy loss due to friction/drag. The presence of damping results in the phase-point falling towards the origin with time. This part of the dynamics is dissipative. Had $\beta<0$, the system would have unstable dynamics with the phase-point diverging to infinity.

In fact, these conditions are the same as the ones which dictate whether a Vector Autoregression is stable or not (remember comparing the moduli of eigenvalues to check if they were > 1 or in other words, lie outside the unit circle?). This connection will be made clearer in another post. Until then, we have a cool gif of the pendulum simulation.

Simulation of the damped pendulum